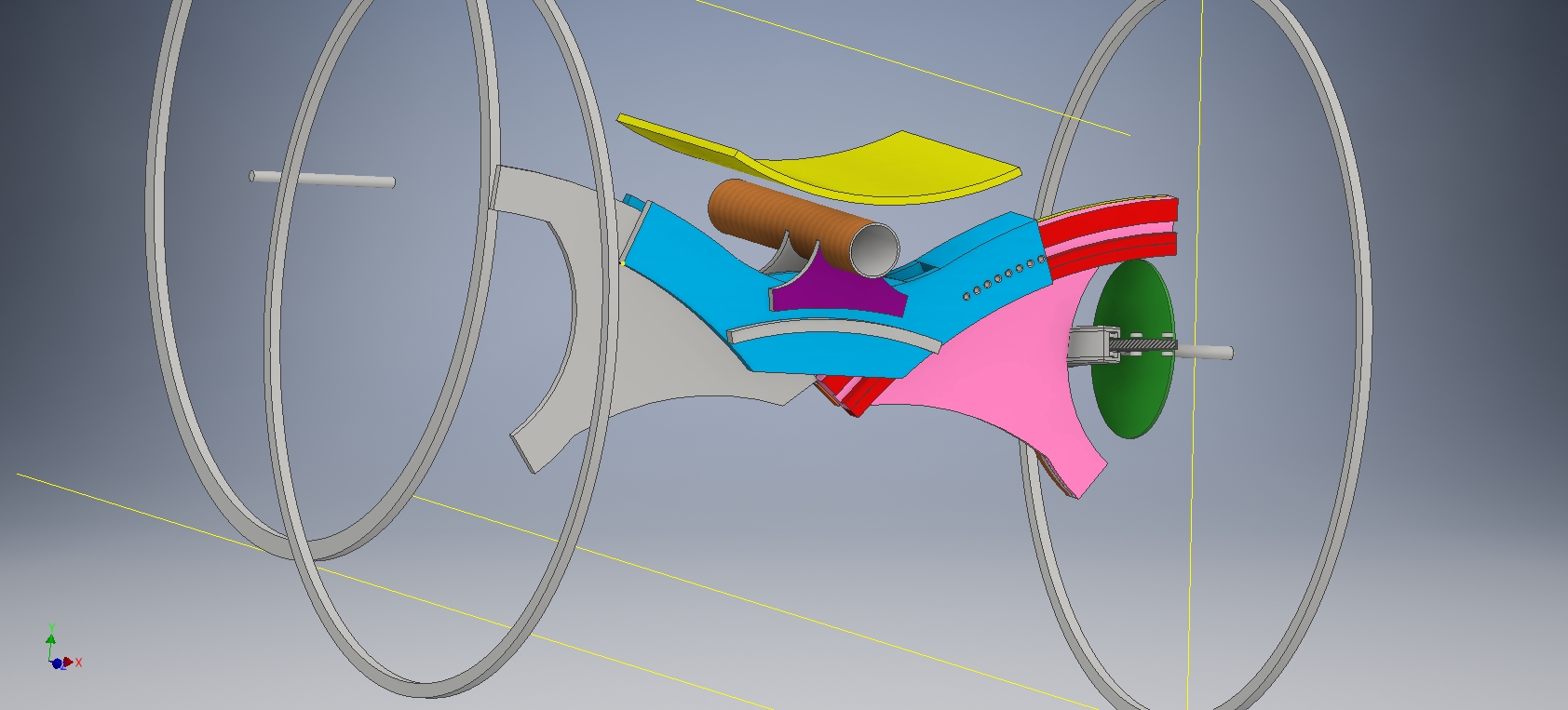
REGULATION DE L’EQUILIBRE pour un cycle oscillant :
L’équilibre régulé par la direction :
- Est obtenu grâce à un apprentissage initial (l’apprentissage du vélo par exemple),
- Ne nécessite pas de polygone de sustentation, il est donc possible pour un deux roues, et autorise une grande amplitude angulaire et une position haute du centre de gravité,
- il est limité par l’adhérence des pneumatiques au sol.
- Est conditionné par l’existence d’un déplacement. La faible vitesse du véhicule rend cet équilibre plus instable, car les deux éléments qui régulent et stabilisent cet équilibre sont respectivement la manipulation de la direction et l’effet gyroscopique (donc la rotation) des roues.
L’équilibre des véhicules pendulaires vrais :
- Est passif, indépendant des réflexes d’équilibration du vestibule humain et instantané,
- Existe en l’absence de déplacement et compense (passivement et instantanément) l’accélération radiale des virages
- Est conditionné par l’existence d’un polygone de sustentation (donc au moins trois points d’appui) et d’un pendule de pilotage,
- Est limité par ce polygone de sustentation : la « sortie » du centre de gravité du pendule de ce polygone rompt l’équilibre. Cette particularité limite l’amplitude angulaire de cet équilibre et la hauteur du centre de gravité du pendule.
- Est bienvenu lorsque le conducteur est inapte à réguler l’équilibre, et à l’arrêt de l’effort
VEHICULE OSCILLANT CLASSIQUE
Description :
Le véhicule oscillant, dont il existe de multiples versions (Leiner, Tripendo, Rartrike, Jetrike, Velotilt, Munzo, Longabike, Maurer… mais aussi Piaggio, Peugeot ou Quadro… pour les scooters ) est représenté par le premier schéma en vue de face sur un terrain plat ( à gauche et en dévers ( à droite).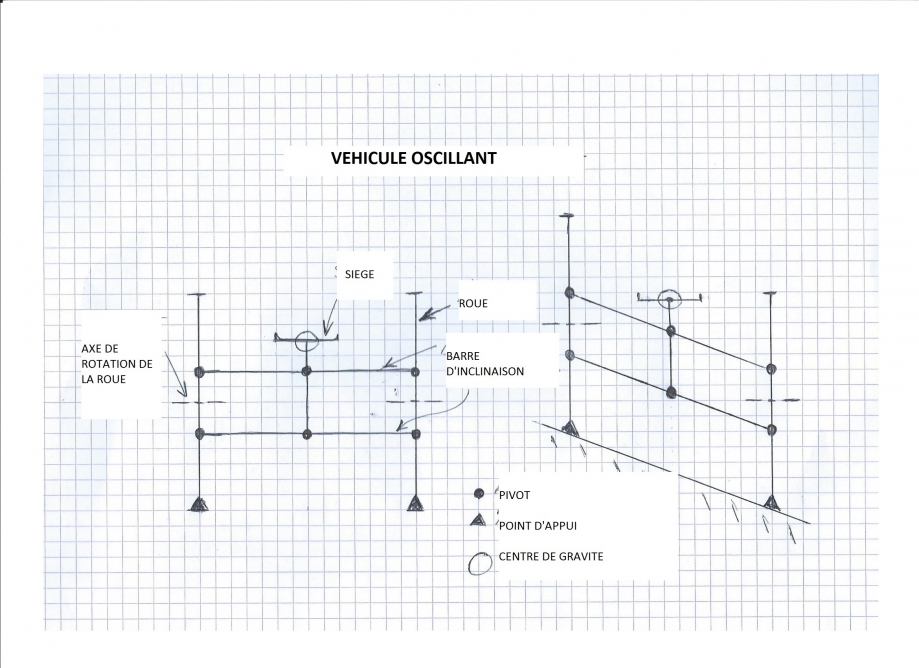
Sur le schéma ci dessus, les deux roues sont des traits verticaux de part et d’autre de la figure.
L’axe de rotation (moyeu) des roues est matérialisé par un trait discontinu horizontal
Les deux traits horizontaux pleins représentent la tringlerie d’inclinaison, et pour simplifier le dessin, cette tringlerie est articulée directement par des pivots sur le trait vertical des roues.
Le pivot de direction n’est volontairement pas représenté
Le centre de gravité du conducteur est un cercle situé sur le siège du véhicule.
Et les points d’appui au sol des roues sont représentés par des triangles.
La position du centre de gravité est déterminée dans ce tricycle par les deux pivots reliant le siège à la tringlerie de direction.
Dans une situation de dévers, (ou bien dans un virage, sous l’action de la force centrifuge), cet équilibre, hautement instable à l’arrêt devient facile à contrôler lors du déplacement par le conducteur grâce à la direction et l’effet combiné du gyroscope des roues en rotation.
Noter que la projection (perpendiculaire) au sol du centre de gravité se déplace lors de l’oscillation vers le haut de la pente (ou bien à l’intérieur du virage dans une situation de braquage).
Limites du système :
Ce déplacement du centre de gravité est parfaitement adapté à la situation d’équilibre des forces exercées sur l’ensemble [tricycle+conducteur] en dévers comme dans les virages (sous l’influence de la force centrifuge), et dans les situations complexes combinant virage et dévers. Cependant, comme je l’ai déjà évoqué, l’adaptation de l’équilibre est directement lié au déplacement du tricycle et à l’habileté de son conducteur qui manipule la direction. Cette compensation exacte de l’action des accélération radiales (gravitationnelle et centrifuge) rend le tricycle stable jusqu’à la limite d’adhérence des pneumatiques.
VEHICULE PENDULAIRE VRAI
Description :
Sur ce deuxième schéma, on utilise les mêmes symboles pour désigner les éléments du tricycle. Peu de constructeurs se sont lancé sur ce type d’appareil, citons une nouvelle fois le Swincar de Mr Pascal Rambeaud. Voir la vidéo ci-dessous…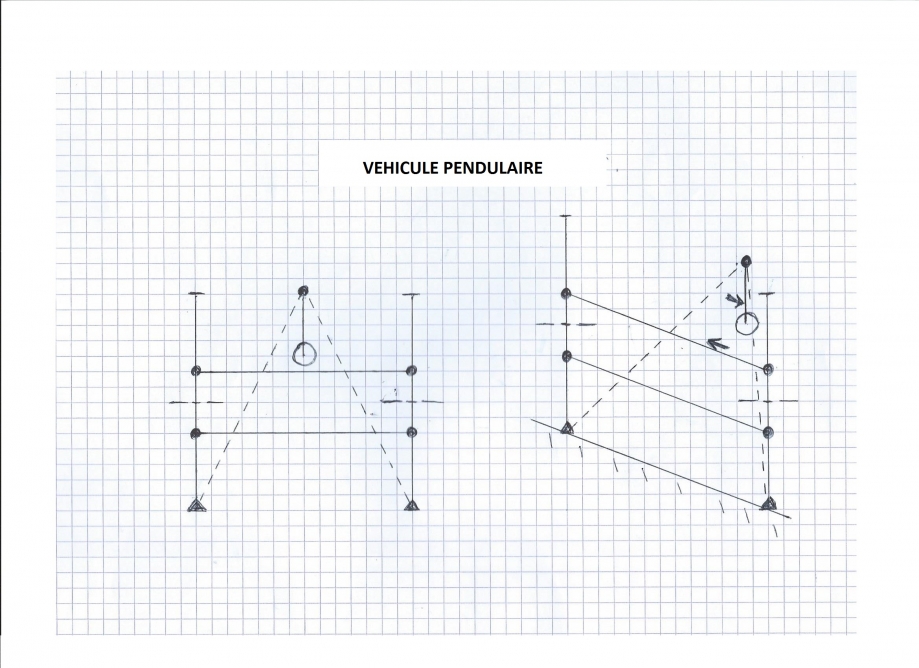
Ce second véhicule comporte un pendule vrai, dont l’axe de suspension est représenté par le pivot en haut du dessin.
Ce point de suspension pendulaire repose par deux bras en pointillés sur les deux points fixes situés sous les roues du véhicule. Les deux bras du pendule déterminent avec les points fixes un triangle isocèle indéformable.
En situation de dévers, le point de suspension du pendule se déplace et entraine un mouvement latéral du centre de gravité (flèche du haut) qui commande un mouvement en sens contraire de la tringlerie d’inclinaison (donc des roues). Le mécanisme de coordination de ces deux mouvements opposés n’est pas représenté.
Pour ce type de véhicule, la projection du centre de gravité au sol se déplace vers le bas de la pente ( ou à l’extérieur du virage lors d’une situation de braquage).
Limites du système :
L’équilibre de ce type de véhicule est instantané, passif et immédiat, ce qui en fait un véhicule très agréable et sécurisant à conduire.
Le déplacement du centre de gravité vers le bas de la pente ou l’extérieur du virage a une limite importante qui est la projection au sol de ce triangle de sustentation du tricycle. Si cette projection dépasse le triangle de sustentation, le tricycle pendulaire se renverse.
Il parait intéressant de créer un véhicule capable de passer de l’équilibre pendulaire à l’arrêt à l’équilibre régulé par la direction en mouvement.
La transition entre ces deux modes de fonctionnement doit être progressive afin de créer ou garder un équilibre pendulaire vrai à l’arrêt / faible vitesse d’une part et obtenir l’équilibre régulé dès que la vitesse le permet.
Nous verrons que le tricycle oscillant mixte corrige ce défaut majeur du tricycle pendulaire vrai et profite des avantages de l’oscillation classique en mouvement (pendule inverse) .
TRICYCLE OSCILLANT MIXTE
Mr Pascal RAMBAUD (Swincar) cite les deux conditions nécessaires pour réaliser un véhicule pendulaire:
- Une référence aux points d’appui au sol, matérialisée (pour son quadricycle) par une projection des axes d’inclinaison des roues sous celles-ci.
- Un pendule constitué d’un ensemble nacelle + conducteur dont le centre de gravité est situé sous un axe pivot longitudinal. Ce pendule constitue un pilote pour l’inclinaison des roues.
Pour la construction d’un véhicule de ce type, que RARTRIKE a appelé le tricycle oscillant mixte, le pivot à guidage linéaire curviligne* va permettre de :
- Projeter l’articulation pivot de l’inclinaison sur un axe sagittal situé sous les roues avant du tricycle grâce à un montage de type « synchronisation de deux arcs semi-circulaires. » Le montage ainsi obtenu définit, avec le point d’appui de la roue arrière, un Plan de référence.
- Reproduire fidèlement l’action d’un pendule en projetant un axe virtuel sagittal de suspension du siège sur lequel repose le conducteur au-dessus du tricycle. Ce siège-pendule à guidage linéaire curviligne de concavité supérieure pilote l’inclinaison des roues.
- réunir tout les systèmes mécaniques dédiés à l’oscillation classique ou pendulaire au centre du véhicule.
(* Brevet invention RARTRIKE)
Un système pendulaire mixte :
A partir de ce tricycle oscillant sur des pivots situés sous les roues, il est possible de bloquer le système pendulaire de pilotage pour prendre le contrôle directionnel de l’inclinaison dès qu’une certaine vitesse l’autorise et obtenir ainsi un tricycle oscillant » classique » dont le pilotage est celui d’un vélo (Think bike).
Tant que le tricycle circule, il fonctionne en équilibre régulé par la direction (et l’effet additif gyroscopique des roues).
Lorsque la vitesse du tricycle devient insuffisante pour un contrôle de l’inclinaison par la direction, le conducteur peut passer en mode pendulaire pour s’arrêter. L’arrêt (le stationnement et le redémarrage) en mode pendulaire est alors possible même si le terrain est en dévers franc.
Ce nouveau mode de fonctionnement est une alternative à la triangulation des tricycles oscillants, dénommée Tricycle oscillant mixte.
Une description détaillée est disponible pour les ingénieurs désireux de pousser plus loin la reflexion dans la section RARTRIKE-Lab. Demandez nous un code d’accès.