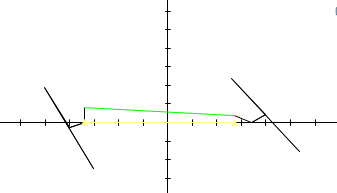
L’objet de cet article est de poser quelques règles simples qui permettent de construire un système de direction pour un tricycle oscillant.
La direction des véhicules obéît à ce qu’on nomme la « condition de Jeantaud », connue aussi sous le nom de triangle d’Ackermann. Rare est le mécanisme qui remplit de façon parfaite cette condition, citons le mécanisme de DAVIES, bien décrit dans le très bon article de Pierre DUYSINX (Université de Liège) sur le sujet : Direction des véhicules (Pierre DUYSINX)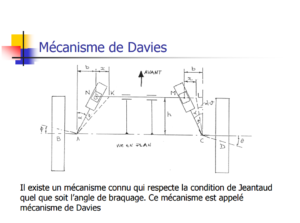
Mais le mieux est l’ennemi du bien, et bien d’autres systèmes, beaucoup plus simples que celui de Davies s’approchent de façon presque parfaite de la condition de Jeantaud d’une part et sont applicables dans certaines conditions aux véhicules oscillants.
Nous avons ainsi exploité les feuilles excel de Mr Peter Eland qui propose une évaluation de la pertinence des dimensions proposées par l’utilisateur par rapport à la condition de Jeantaud.
Géométrie du système de direction des tricycles (Peter Eland)
D’une façon générale, la tringlerie de direction doit épouser les modifications géométriques du système oscillant d’une part et respecter la condition de Jeantaud d’autre part.
RARTRIKE PGL
Il existe des Schémas impossibles. L’exemple le plus démonstratif dans notre expérience est celle du tricycle RARTRIKE PGL.
Ce tricycle, construit sur le modèle mécanique de Mr Alan MAURER, comporte un pivot de direction-inclinaison. Les deux motions sont dépendantes. Il s’agit d’un pivot de direction à angle de chasse variable. Lorsque ce pivot est vertical, il dirige le tricycle, lorsqu’il est horizontal, il fait s’incliner le tricycle. Le tricycle d’Alan Maurer propose un contrôle par le conducteur de cet angle de chasse par deux leviers. Le maintien d’un angle de chasse intermédiaire permet d’obtenir une combinaison de braquage-inclinaison combinés. Ce qui pose problème dans cette configuration, c’est que le tricycle tourne du côté où il se penche. Or dans certaines situations, cette interdépendance des deux systèmes direction et inclinaison est inadaptée, notamment le dévers, lorsque le tricycle doit aller tout droit ou tourner vers la pente. Autre élément à considérer, c’est que le système d’inclinaison fonctionne sur le modèle d’un parallélogramme déformable, alors que pour la direction d’un tricycle, il s’agit plutôt d’un trapèze déformable. L’évolution d’une géométrie vers l’autre au cours de la variation de l’angle de chasse est sans doute possible, mais très complexe à réaliser. L’utilisation du RARTRIKE PGL nous a donc appris une chose : Direction et Inclinaison doivent être indépendantes. Pour le RARTRIKE PGL, nous avons utilisé un système « 4 bras » simple et nous avons bloqué l’angle de chasse à une valeur élevée, ce qui fait que le tricycle tourne et s’incline du même côté dans des proportions constantes.
RARTRIKE PJE
Pour le RARTRIKE PJE le système directionnel suit la géométrie des bras oscillant, il s’agit d’un système de type » conventionnel » dont les bielettes sont dans le plan des bras oscillants.
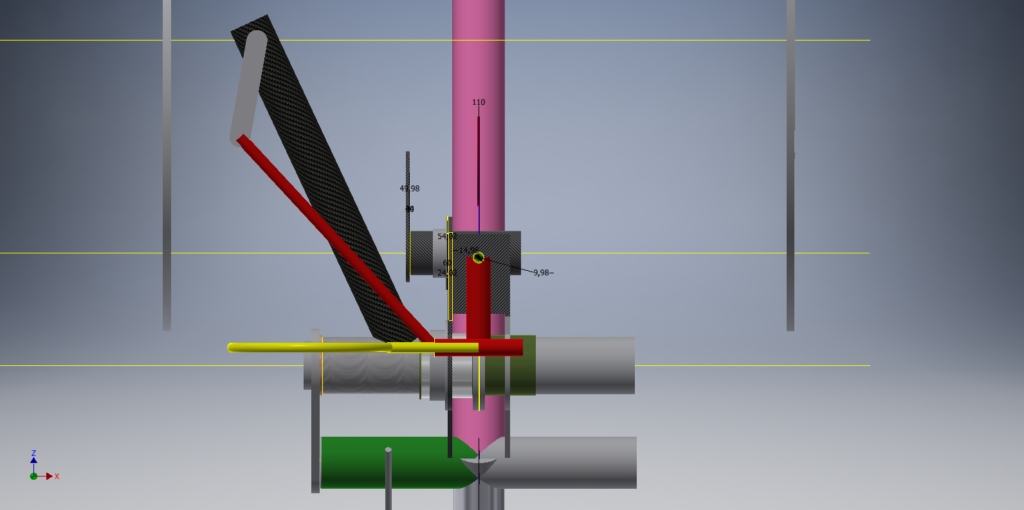DIRECTION RARTRIKE PJE Vue inférieure : la tringlerie de direction est en rouge, la structure en « T » inversé pivote autour du point jane centré de vert
DIRECTION RARTRIKE PJE vue inféro-latéralegauche où l’on peut distinguer le « guidon » jaune du tricycle
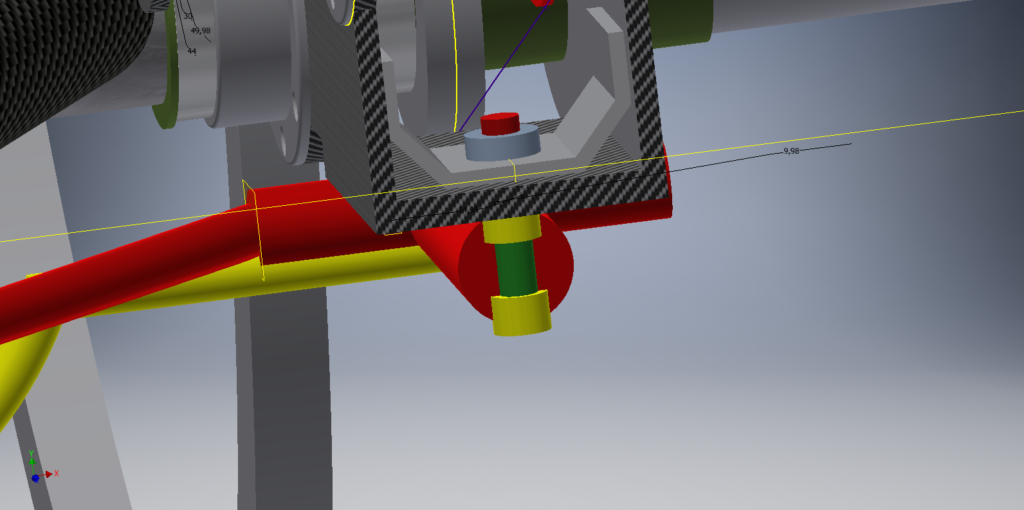DIRECTION RARTRIKE PJE Vue antérieure : les deux roulements en jaune du pivot de direction, fixés à la face inférieure de la boite de vitesse.
TRICYCLE OSCILLANT ALPIN (ALPIN LEANING TRIKE)
Pour le Tricycle Oscillant Alpin (Alpin Leaning Trike) La tringlerie de direction évolue dans un plan parallèle au sol et de façon synchrone aux ailes oscillantes. C’est un système « 4 bras » classique.
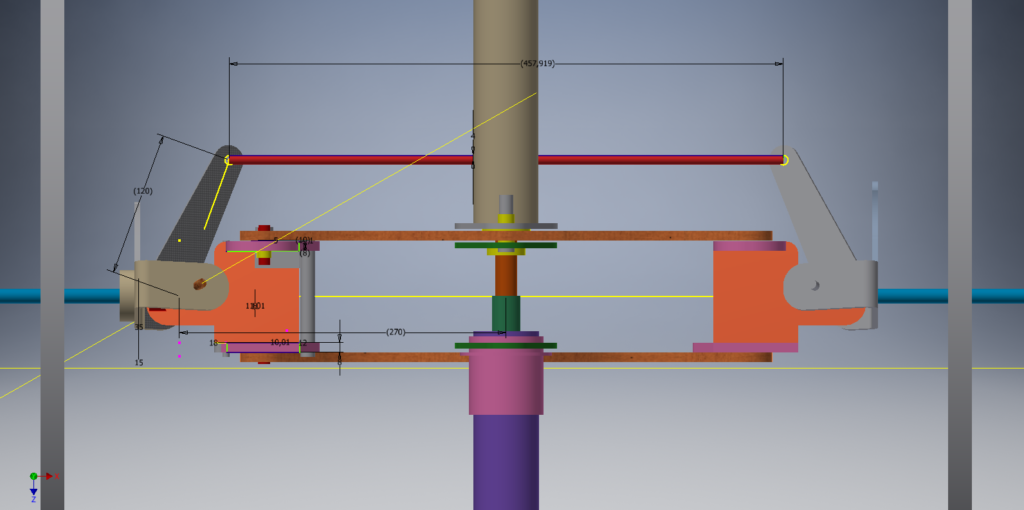
TINGLERIE DIRECTION ALPIN LEANING TRIKE vue supérieure
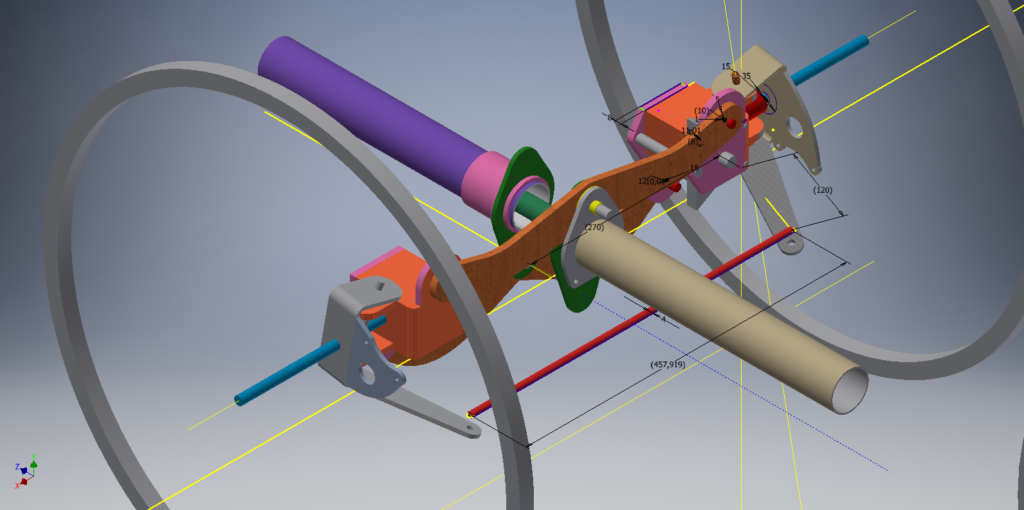
DIRECTION ALPIN LEANING TRIKE vue postero-latérale
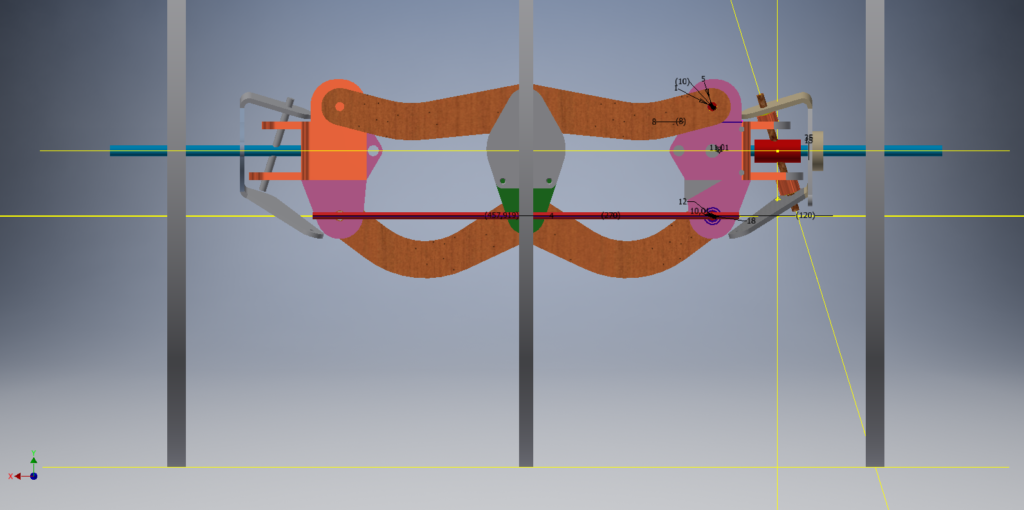
DIRECTION ALPIN LEANING TRIKE vue postérieure